Research Projects
2025
2024
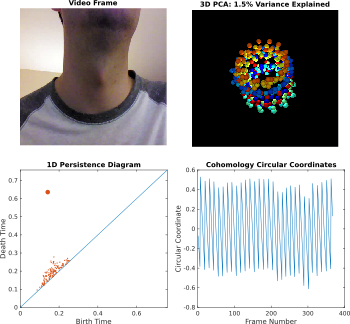
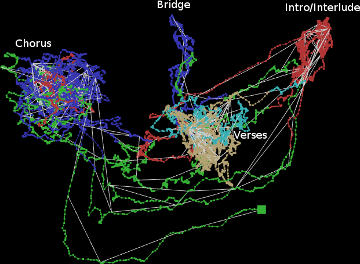
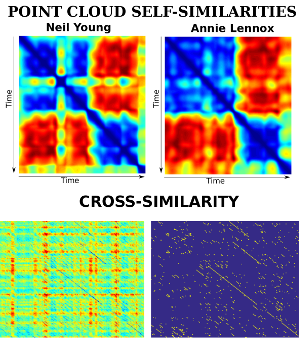
The Concatenator: A Bayesian Approach To Concatenative Musaicing. Christopher J. Tralie, Ben Cantil ("Encanti"), Proceedings of the 25th Conference of the International Society for Music Information Retrieval (ISMIR 2024).
- Paper link
- Code link
- Quick explanatory video
- Supplementary audio, videos, etc
- DataMind Audio product based on this technology
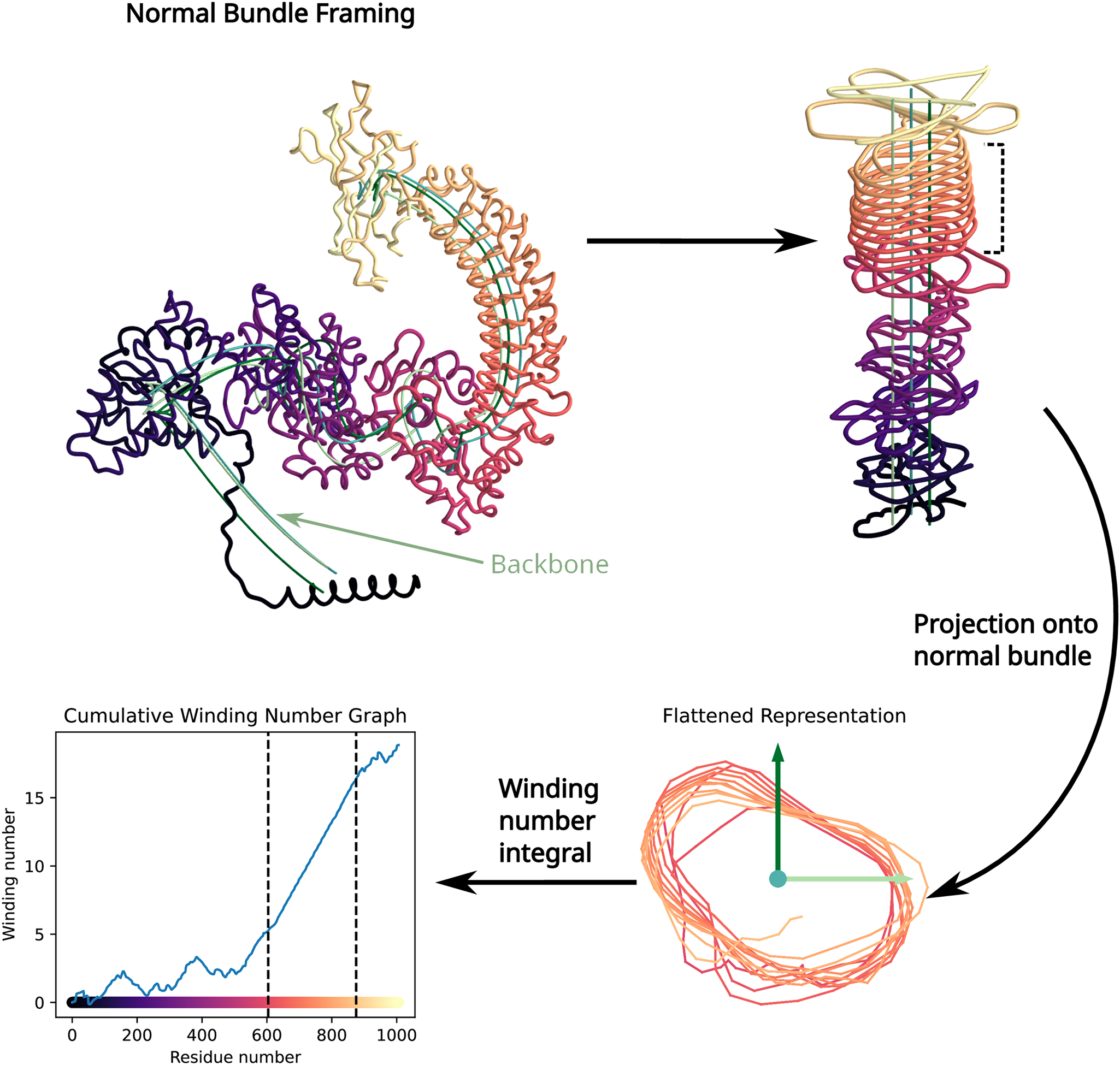
2023
Godzilla Onions: A Skit and Applet to Explain
Euclidean Half-Plane Fractional Cascading. Rich Berger, Vincent Ha, David Kratz, Michael Lin, Jeremy Moyer, Christopher J. Tralie
Symposium on Computational Geometry (SOCG) Multimedia
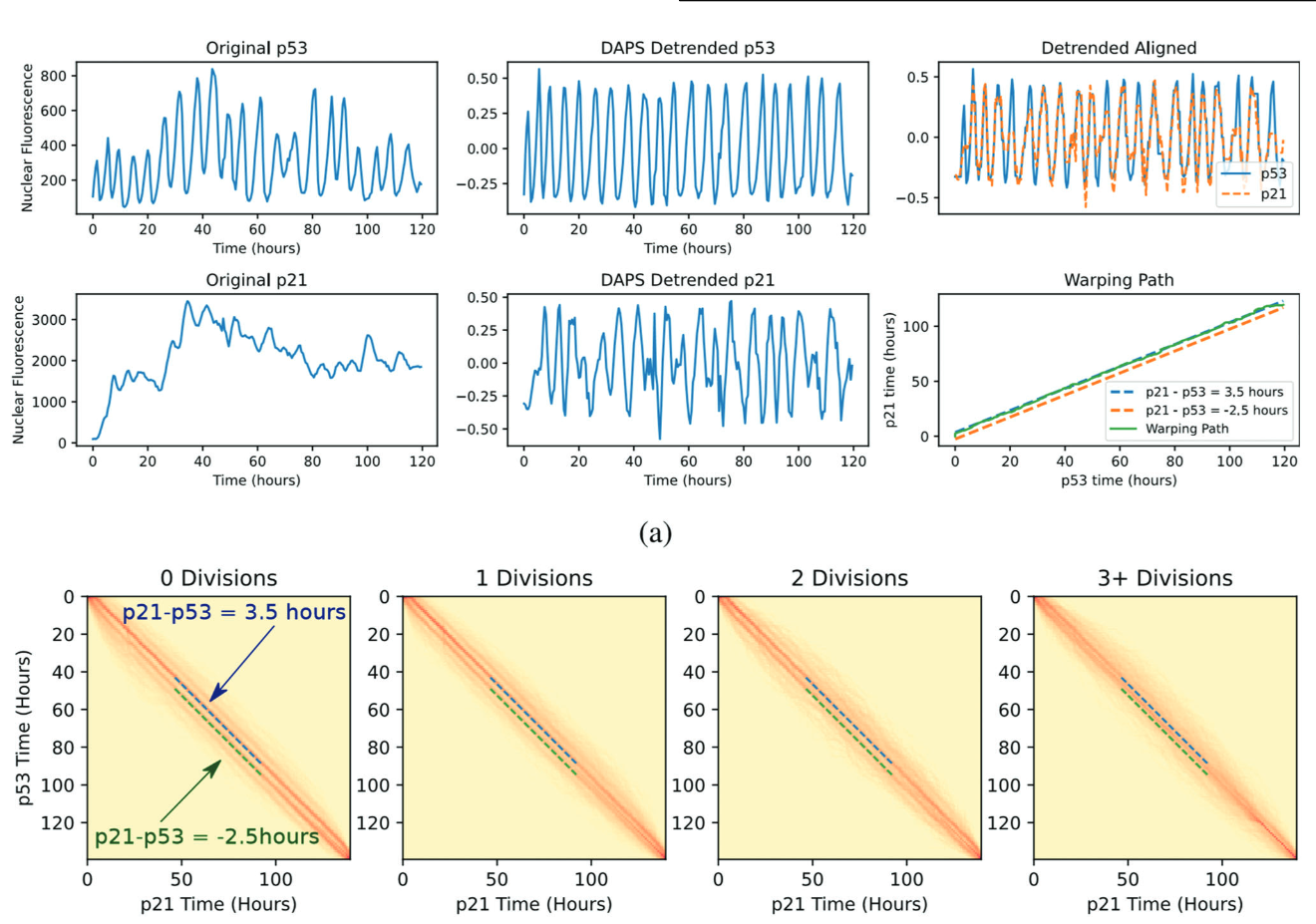
Long-term p21 and p53 dynamics regulate the frequency of mitosis events and cell cycle arrest following radiation damage. Anh Phong Tran, Christopher J. Tralie, José Reyes, Caroline Moosmüller, Zehor Belkhatir, Ioannis G. Kevrekidis, Arnold J Levine, Joseph O. Deasy, Allen R. Tannenbaum. Nature Cell Death And Differentiation.
2021
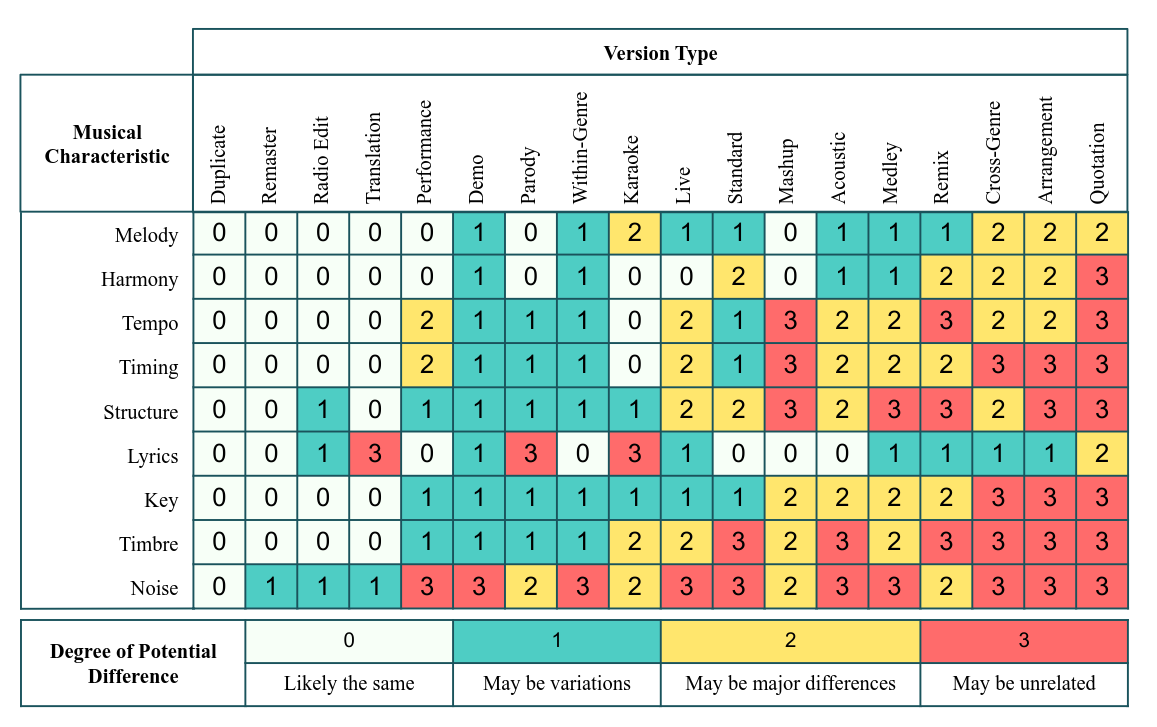
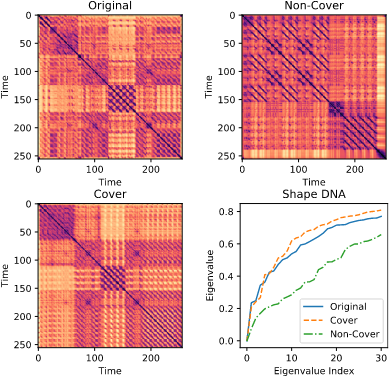
Audio-based musical version identification: Elements and challenges. Furkan Yesiler, Guillaume Doras, Rachel Bittner, Christopher J. Tralie, Joan Serrà
IEEE Signal Processing Magazine
- Paper link
- Examples of versions catalogued by Rachel Bittner
www.facejam.app: Facial Expressions for Musical Expression. Christopher J. Tralie, Parker Fairchild
22nd International Society for Music Information Retrieval Conference Late Breaking Demo Session
2020
Periodicity Scoring of Time Series Encodes Dynamical Behavior of the Tumor Suppressor p53. Caroline Moosmüller, Christopher J. Tralie, Mahdi Kooshkbaghi, Zehor Belkhatir, Maryam Pouryahya, José Reyes, Joseph O. Deasy, Allen R. Tannenbaum, Ioannis G. Kevrekidis. 24th International Symposium on Mathematical Theory of Networks and Systems (MTNS 2020).
2019
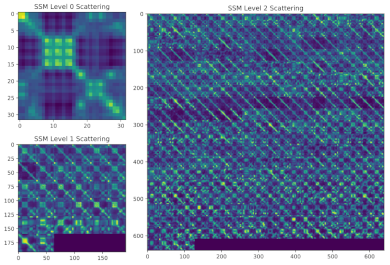
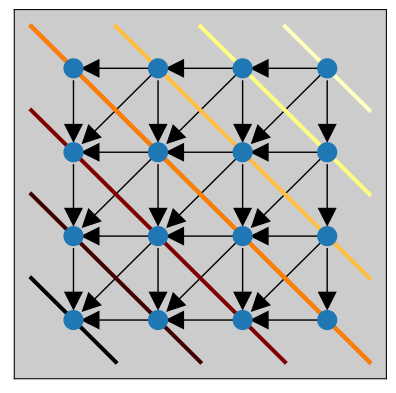
Multi-scale Geometric Summaries for Similarity-based Sensor Fusion. Christopher J. Tralie, Paul Bendich, and John Harer. IEEE Aerospace Conference, 2019, Big Sky, Montana.

2018
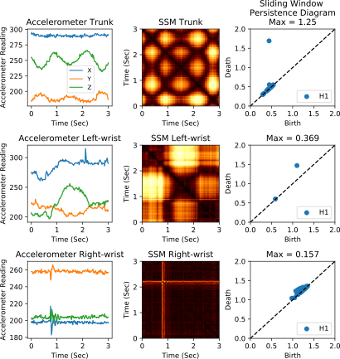
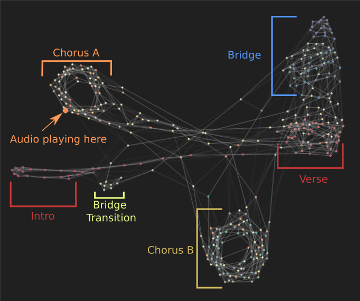


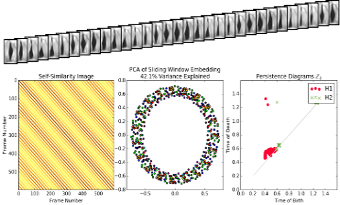
2017
Self-Similarity Based Time Warping. Christopher J. Tralie. arXiv preprint arXiv:1711.07513, 2017.
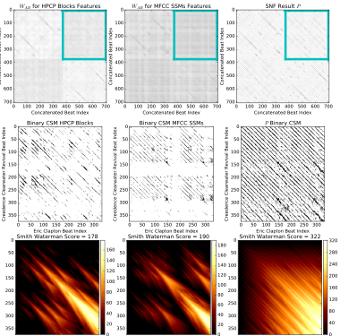
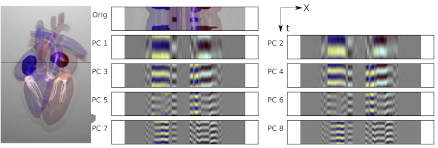
Geometric Multimedia Time Series. Christopher J. Tralie. Dissertation, Duke University Department of Electrical And Computer Engineering
2016