Classes
I am no longer serving as a professor, but when I taught, my teaching specialties were in CS theory (data structures, theory of computation) and CS applications (computer graphics, digital music processing, and artificial intelligence). Over the years, I made myriad open source teaching materials and videos on my Youtube Channel, and I was twice recognized by the Association for Computing Machinery (ACM) in the prestigious "nifty assignments" track.
Now I make videos on YouTube for even wider audiences.
Below is an archive of the courses I taught:
Spring 2025
CS 372: Digital Music Processing (20 Students)
CS 475: Computer Networks (23 Students)
CS 391: Research Independent Study on JPEG for Artistic Purposes (1 Student)
Fall 2024
CS 271: Algorithms And Data Structures (20 Students)
CS 476: Computer Graphics (24 Students)
CIE 100: Common Intellectual Experience I (16 Students)
Spring 2023
I am on pre-tenure sabbatical leave from regular teaching this spring, and I am mostly focused on research. But I will be presenting this assignment from CS 174 at SIGCSE 2024 this spring.
-
CS 391: Research Independent Study (3 Students)
Hamiltonian Paths Through The Associahedron
Audio Watermarking
CS 382: Spring Internship (2 Students)
Fall 2023
CS 271: Algorithms And Data Structures (30 Students)
CS 373: Theory of Computation (12 Students)
CS 477: Artificial Intelligence And Machine Learning (22 Students)
-
CS 382: Summer Internship (3 Students)
Spring 2023
CS 174: Object Oriented And Systems Programming (21 Students)
IDS 301: Problem Solving And Analysis with Python (3 Students)
CS 372: Digital Music Processing (24 Students)
-
CS 382: Spring Internship (1 Student)
Fall 2022
CS 174: Object Oriented And Systems Programming (12 Students)
CS 271: Algorithms And Data Structures (16 Students)
CS 476: Computer Graphics (21 Students)
CS 382: Summer Internship (5 Students)
Spring 2022
CS 174: Object Oriented And Systems Programming (12 Students)
CIE 200: Common Intellectual Experience (16 Students)
CS 371: Algorithms And Data Structures (24 Students)
CS 382: Research Independent Study (1 Student)
-
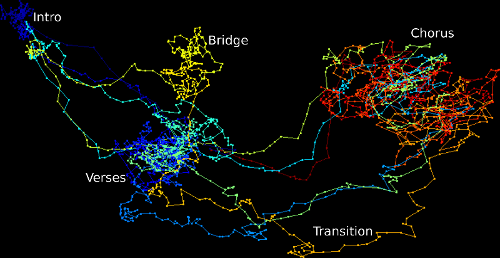
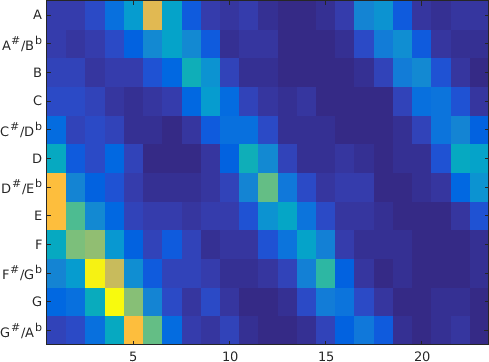
Traveling Salesperson Tunes: A New Method for Image Musification
-
-
CS 391: Research Independent Study (1 Student)
-
Augmented Reality for Counterpoint Education
-
-
CS 491: Honors Research Independent Study (1 Student)
-
A Data Driven Approach to Structure-Based Large Scale Audio Version Identification
-
-
CS 381: Spring Internship (1 Student)
-
CS 382: Spring Internship (1 Student)
Fall 2021
CS 373: Theory of Computation (16 Students)
CS 477: Artificial Intelligence And Machine Learning (22 Students)
-
CS 391: Research Independent Study (3 Students)
Augmented Reality for Counterpoint Education
3D Video Amplification of Hidden Periodic Motions
-
CS 382: Fall Internship (1 Student)
Spring 2021
CS 371: Algorithms And Data Structures (26 Students)
CS 472: Digital Music Processing (15 Students)
CS 391: Research Independent Study (2 Students)
Web Virtual Reality for Everyone
Ursinus Smokestack 3D Annotation Interface
Fall 2020
CS 174: Object-Oriented Programming (19 Students)
CS 476: Computer Graphics (12 Students)
CS 394: Research Independent Study (1 Student)
Statistical Machine Translation of Lingala Facile
Spring 2020
CS 173: Intro To Computer Science (33 Students)
IDS 301: Problem Solving And Analysis with Python (12 Students)
-
CS 392: Research Independent Study (1 Student)
Nonrigid Reconstruction of 3D Shapes
-
CS 394: Research Independent Study (1 Student)
Dimension Reduction with Eilenberg-MacClane Coordinates
Fall 2019
Math 111: Calculus 1 (16 Students)
CS 476: Computer Graphics (11 Students)
CS 391 Research Independent Study (1 Student):
FaceJam: Javascript Facial Expressions for Musical Expression
CS 394 Research Independent Study (2 Students):
-
Self-Similarity Scattering Transforms for Large Scale Audio Cover Song Identification
-
Parallel Dynamic Time Warping for Musical Audio Synchronization
-
Spring 2016
CS/Math 290: Digital 3D Geometry
As part of the Bass Instructor of Record Fellowship, I designed a new undergraduate course at Duke University cross-listed between computer science and math during the spring 2016 semester. The course was a ground up approach to 3D geometry with a statistics and signal processing focus. Assignments were in Javascript/WebGL and Python/Numpy, including sound modeling in virtual acoustic environments, rotation modeling with Euler angles and quaternions, 3D shape statistics ("Shape Google"), 3D shape alignment, and spectral mesh processing. This course was rated in the top 5% of courses university wide that semester in "quality of course/intellectual stimulation," based on student evaluations.
Click here to see the midterm exam I designed. Below are some highlights from the course syllabus
Guest Lectures / Labs on Topological Data Analysis
As a member of the Harer group both as a Ph.D. student and a postdoc, I have developed a lot of teaching materials on toplogical data analysis (TDA), including tons of demos and code, which I have used at numerous workshops and guest lectures. Below are a few highlights:
- TDA Labs from The Ground Up
This is a work in progress, which I have used at multiple workshops, including Mathematical Methods for High Dimensional Data Analysis (Summer 2016, Technical University Munich), Summer@ICERM 2017 (Brown University), and Topological Data Analysis And Persistent Homology (Summer 2018, Levico Terme, Italy)
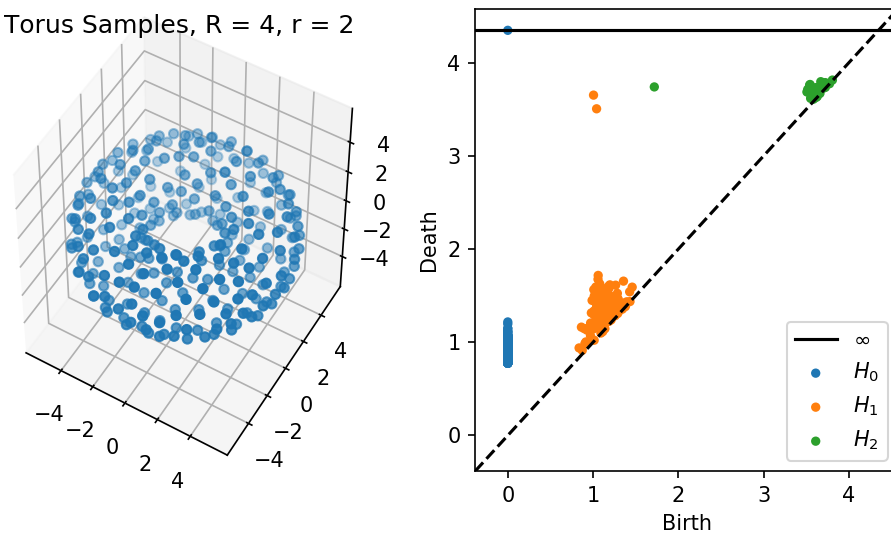
- ripser.py
I worked with Nathaniel Saul to create a Python interface to the fast ripser library for persistent homology. As part of this, I created some pedagogical notebooks to show some lesser known features, including sparse filtrations and arbitrary field coefficients.
- Math 412 Guest Lecture on 0D persistent homology 9/6/2018
ripser.py on synthetic shapes
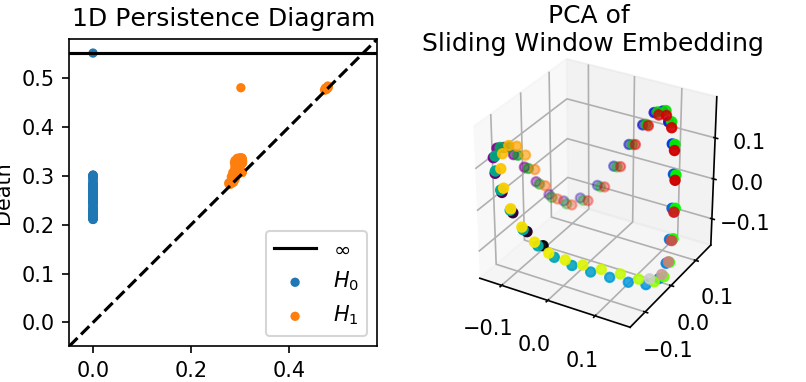
Sliding window of periodic videos
Lower Star Filtrations for Nonrigid 3D Shapes
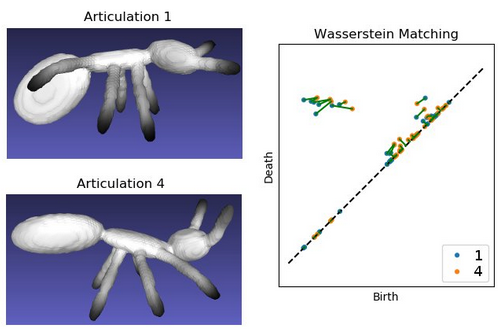
Image Patches on the projective plane using Projective Coordinates

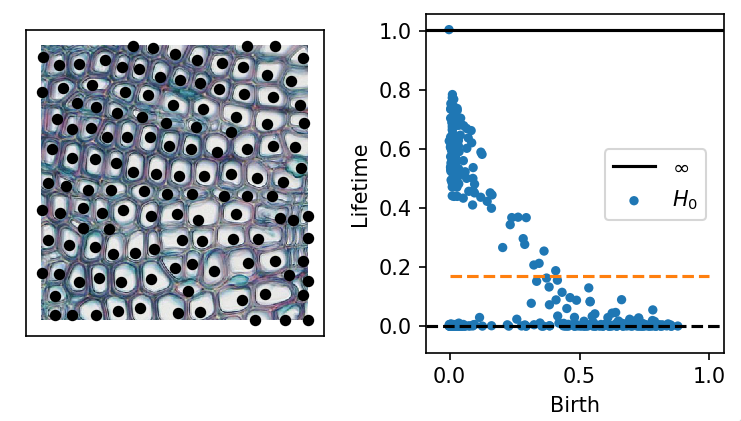
Lower star filtrations on an image to identify plant cell locations
IID Data Expeditions Labs, Fall 2014
I designed two different labs using music to get undergraduates interested in signal processing. One was a more traditional lab on pitch extraction in a digital signal processing course (ECE 381), and the other one was using novel topological techniques from my research to analyze the "shape" of the music. Click on the links below to view the assignments.
This is a work in progress, which I have used at multiple workshops, including Mathematical Methods for High Dimensional Data Analysis (Summer 2016, Technical University Munich), Summer@ICERM 2017 (Brown University), and Topological Data Analysis And Persistent Homology (Summer 2018, Levico Terme, Italy)
I worked with Nathaniel Saul to create a Python interface to the fast ripser library for persistent homology. As part of this, I created some pedagogical notebooks to show some lesser known features, including sparse filtrations and arbitrary field coefficients.