#24: Geometric Set Cover-0

Click here to view the PDF version of this document
Overview
The purpose of this lecture is to cover a few classic combinatorial optimization problems, including set cover, hitting set, and independent set, in a geometric context. Though the optimal set cover and hitting set problems are NP-hard, results from ![]() -nets help to give good approximation bounds for these algorithms for simpler set systems that arise in a geometric context.
-nets help to give good approximation bounds for these algorithms for simpler set systems that arise in a geometric context.
The notes begin with some preliminary definitions of the dual range space and of the algorithms, and several results from ![]() -nets are reviewed. Then, a modified, weighted version of an
-nets are reviewed. Then, a modified, weighted version of an ![]() -net is presented which leads to an approximation algorithm for the hitting set and set cover. After this, a new randomized hitting set algorithm with better bounds is presented, which was discovered by our very own T.A. Jiangwei Pan and professor Pankaj Agarwal. Finally, some basic ideas for independent set are shown in a geometric context
-net is presented which leads to an approximation algorithm for the hitting set and set cover. After this, a new randomized hitting set algorithm with better bounds is presented, which was discovered by our very own T.A. Jiangwei Pan and professor Pankaj Agarwal. Finally, some basic ideas for independent set are shown in a geometric context
Throughout, I also highlight several open problems that were mentioned in class.
Dual Range Spaces
Definitions
Let
![]() be a range space on the set
be a range space on the set ![]() . Then
. Then
is the dual range space associated with ![]()
In other words, the space becomes the set of ranges, and the ranges become sets of ranges that hit an ![]() . A slightly easier conceptualization of a range space for this purpose is a bipartite graph, where one set is the elements in
. A slightly easier conceptualization of a range space for this purpose is a bipartite graph, where one set is the elements in ![]() and the other set is the ranges, and there's a line between
and the other set is the ranges, and there's a line between ![]() and
and ![]() if
if ![]() . The dual range space simply switches the roles of the two sets in the graph. Figure 1 shows an example with this construction.
. The dual range space simply switches the roles of the two sets in the graph. Figure 1 shows an example with this construction.
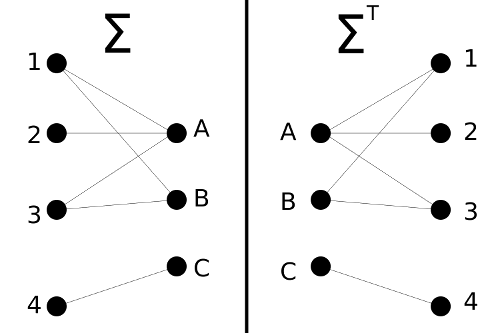 |
Note also that if one constructs an incidence matrix ![]() for the range space out of this bipartite graph, then
for the range space out of this bipartite graph, then ![]() represents an incidence matrix for the dual range space. This makes the transpose symbol a natural choice for denoting the dual range space.
represents an incidence matrix for the dual range space. This makes the transpose symbol a natural choice for denoting the dual range space.
Geometric Example
One way to visualize dual range spaces in a geometric context is with points and rectangles. Define the following objects:
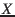 : Finite set of points in
: Finite set of points in
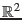
 : A finite set of
: A finite set of 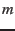 rectangles
rectangles
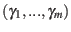
-
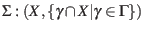
In other words, for each rectangle, create a range comprised of the points that are contained within that rectangle
-
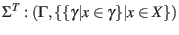
In other words, for each point, create a range out of the set of rectangles that contain it
Figure 2 shows an example of such a space.
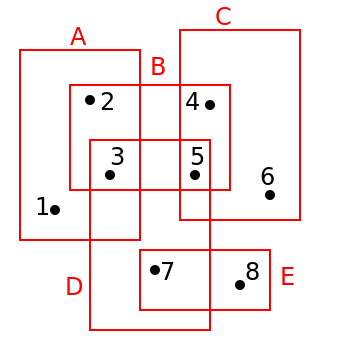 |
Geometric Hitting Set and Set Cover
Definitions
For the range space
![]() ,
,
![]() is a hitting set of
is a hitting set of ![]() if
if
For the range space
![]() ,
,
![]() is a set cover of
is a set cover of ![]() if
if
Note that the hitting set of a range space ![]() is the same as a set cover of
is the same as a set cover of ![]() . The goal is to find the smallest sized hitting set or set cover. Note also that the hitting set is closely related to an
. The goal is to find the smallest sized hitting set or set cover. Note also that the hitting set is closely related to an
![]() net. To see this, recall the definition of an
net. To see this, recall the definition of an
![]() net
net
![]() is an
is an
![]() net of
net of ![]() if
if
![]()
If
![]() in the definition of the the
in the definition of the the ![]() -net, where
-net, where ![]() for the ranges space
for the ranges space
![]() , then the
, then the ![]() -net is certainly a hitting set for all of the ranges, because every range has size at least 1. Though the
-net is certainly a hitting set for all of the ranges, because every range has size at least 1. Though the ![]() is quite small in this case, and it is only related to
is quite small in this case, and it is only related to ![]() , not to the optimal sized hitting set. Still, if one can improve the bound on
, not to the optimal sized hitting set. Still, if one can improve the bound on ![]() ,
, ![]() -nets may be useful for set systems of bounded VC-dimension because of the following theorem
-nets may be useful for set systems of bounded VC-dimension because of the following theorem
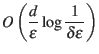
Thus, the hope is to come up with better approximation algorithms for simple set systems using this theorem. As an example of where this may be useful, return to the ranges space with points and rectangles in Section 2.2. In fact, for this range space, an even better bound of size
![]() has been shown recently in [AES10], while the
has been shown recently in [AES10], while the ![]() -net of the dual range space is still
-net of the dual range space is still
![]() with constant probability.
with constant probability.
As a side note, this implies that there is actually a gap in the bounds for computing set cover and the hitting set if ![]() -nets are used for the approximation.
-nets are used for the approximation.
An Approximation Algorithm
As mentioned before, the goal is to somehow reduce the hitting set to an ![]() -net. The main issue with the
-net. The main issue with the ![]() -net is that it is only guaranteed to cover heavy (high cardinality) ranges, but the hitting set requires all ranges to be covered, so before
-net is that it is only guaranteed to cover heavy (high cardinality) ranges, but the hitting set requires all ranges to be covered, so before ![]() had to be set to a very small value
had to be set to a very small value
![]() . To make this more convenient for the hitting set application, modify the definition of an
. To make this more convenient for the hitting set application, modify the definition of an ![]() -net to include weights for each element, so that small sets can effectively be given larger weights:
-net to include weights for each element, so that small sets can effectively be given larger weights:
For a range set
![]() , define a map
, define a map
And extend this maps to sets ![]() so that
so that
Then
![]() is a weighted
is a weighted ![]() -net of
-net of
![]() if
if
![]()
Also say that ![]() is
is ![]() -light if
-light if
![]()
Use this modified definition to devise an algorithm that estimates the weights ![]() for a range space
for a range space
![]() that will lead to a good hitting set approximation with an
that will lead to a good hitting set approximation with an ![]() -net. The algorithm is as follows:
-net. The algorithm is as follows:
The algorithm is very simple, but the analysis requires some tricks. To analyze this algorithm, let ![]() be
be ![]() after
after ![]() iterations. Find an upper bound and a lower bound for
iterations. Find an upper bound and a lower bound for ![]() . Also let
. Also let ![]() be an optimal hitting set algorithm of size
be an optimal hitting set algorithm of size ![]() .
.
- To find an upper bound, observe that at each iteration, the weights of an
 -light range
-light range  are doubled. Since by definition
are doubled. Since by definition
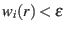 ,
,
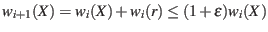
Since all of the weights start off at 1,
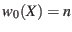 . Thus, the upper bound is
. Thus, the upper bound is
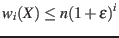
- To find a lower bound, examine what happens to
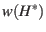 after each iteration. Note that at each iteration, at least one element in
after each iteration. Note that at each iteration, at least one element in 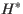 is doubled in weight. For the first
is doubled in weight. For the first 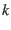 iterations, the minimum happens if these changes are spread out, so that a different element is doubled each time. Thus,
iterations, the minimum happens if these changes are spread out, so that a different element is doubled each time. Thus,
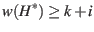
Let
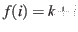 (spread the changes out evenly), and let
(spread the changes out evenly), and let
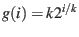 . Then
. Then
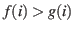 over
over ![$ [0, k]$](img66.png) , because
, because
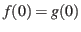 ,
,
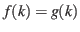 ,
,
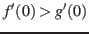 , and they are both convex functions. Also, each group of
, and they are both convex functions. Also, each group of  iterations after the first
iterations after the first  (for
(for 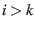 ), it is also true that the minimum is achieved by spreading the elements out. Therefore, the lower bound over all
), it is also true that the minimum is achieved by spreading the elements out. Therefore, the lower bound over all 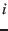 elements doubled in weight is
elements doubled in weight is
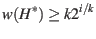
To get ![]() involved in the upper bound, let
involved in the upper bound, let
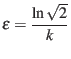
, a choice which will become clear in a moment. Then
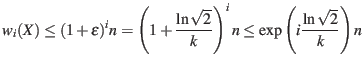
Since
![]() ,
,
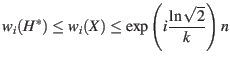
Now combine the lower bound and the upper bound on ![]()
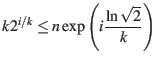
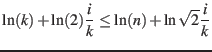
In this step it is clear how clever the choice of
![]() is (it allows us to subtract
is (it allows us to subtract
![]() from both sides of the inequality while maintaining a nonzero factor of
from both sides of the inequality while maintaining a nonzero factor of
![]() on the left side)
on the left side)
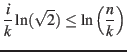
The analysis so far has assumed the size of the optimal hitting set ![]() , is known, but that information is not actually available up front. To estimate
, is known, but that information is not actually available up front. To estimate ![]() , pick start with a small value of
, pick start with a small value of ![]() (say 1), and do an exponential binary search, doubling
(say 1), and do an exponential binary search, doubling ![]() if the algorithm above doesn't converge in
if the algorithm above doesn't converge in
![]() steps.
steps.
When the algorithm finally terminates, the ![]() -net of the weighted range space
-net of the weighted range space
![]() is an
is an
![]() of the optimal hitting set of the ranges. In practice, to transform the weighted
of the optimal hitting set of the ranges. In practice, to transform the weighted ![]() -net to an unweighted
-net to an unweighted ![]() -net so that ordinary
-net so that ordinary ![]() -net algorithms can be run, simply replicate the elements in
-net algorithms can be run, simply replicate the elements in
![]() by their weights (this is why it was important that
by their weights (this is why it was important that ![]() be positive integer weights).
be positive integer weights).
Jiangwei and Pankaj's Approximation Algorithm
Let ![]() be the number of indices
be the number of indices
![]() where
where
![]() . Then a
. Then a ![]() -net of the weighted range space
-net of the weighted range space
![]() , is an
, is an ![]() approximation of the optimal hitting set. More details can be found in [AP14], particularly in Section 4 of that paper.
approximation of the optimal hitting set. More details can be found in [AP14], particularly in Section 4 of that paper.
Geometric Independent Set
The independent set problem asks for the largest set system such that each set is pairwise disjoint. This problem appears to be harder than hitting set and set cover to approximation. In particular, for some independent sets of size ![]() , the best known polynomial approximation algorithm returns a set system within
, the best known polynomial approximation algorithm returns a set system within ![]() size of the optimal.
size of the optimal.
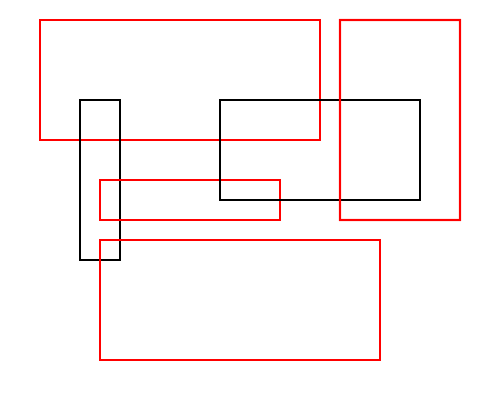 |
One geometric example is, given a set of axis-parallel rectangles ![]() , find the largest subset
, find the largest subset
![]() such that
such that
![]() . An example is shown in Figure 3. An application of this example is to figure out how many city labels it is possible to display on a map without too much clutter (reduce to this problem by putting a bounding rectangle around each city label).
. An example is shown in Figure 3. An application of this example is to figure out how many city labels it is possible to display on a map without too much clutter (reduce to this problem by putting a bounding rectangle around each city label).
With the simpler example where all rectangles are unit-sized squares, a constant-factor approximation is possible with a simple greedy algorithm which takes a random square and removes the squares that intersect it, and repeats until there are no pairwise intersections. To extend this to squares of different sizes, do the same, but choose the squares to check in increasing order of size.
For rectangles, a ![]() approximation is possible with the following greedy algorithm:
approximation is possible with the following greedy algorithm:

It is also possible to approximate this problem by formulating it as an integer linear programming and then rounding, but this is slower.
Bibliography
- AES10
-
Boris Aronov, Esther Ezra, and Micha Sharir.
Small-size eps-nets for axis-parallel rectangles and
boxes.
eps-nets for axis-parallel rectangles and
boxes.
SIAM Journal on Computing, 39(7):3248-3282, 2010. - AP14
-
Pankaj K Agarwal and Jiangwei Pan.
Near-linear algorithms for geometric hitting sets and set covers.
Proceedings of the 30th Annual Symposium on Computational Geometry, 2014. - HP11
-
Sariel Har-Peled.
Geometric approximation algorithms, volume 173.
American Mathematical Soc., 2011.
About this document ...
This document was generated using the LaTeX2HTML translator Version 2008 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 1 -font_size 16pt Notes_lec22.tex
The translation was initiated by Chris Tralie on 2014-05-03
Chris Tralie 2014-05-03blog comments powered by Disqus

